


Next: Evolving Neural Networks
Up: GBML Areas
Previous: Genetic Programming
Contents
Subsections
3.3 Evolving Ensembles
Ensembles, also called Multiple Classifier Systems and Committee
Machines, is the field which studies how to combine predictions from
multiple sources. Ensemble methods are widely applicable to
evolutionary systems where a population provides multiple
predictors. Ensemble techniques can be used with any learning method,
although they are most useful for unstable learners, whose hypotheses
are sensitive to small changes in their training. Ensembles can be
heterogeneous (composed of different types of predictors) in which case
they are called hybrid ensembles. Relatively few studies of
hybrid systems exist [37] but see
e.g. [313,72,69] for examples. Ensembles
some enjoy good theoretical foundations [37,279],
perform very well in practice [64] and were identified
by Dietterich as one of four current directions for machine learning
in 1998 [80].
While the key advantage of using ensembles is better test set
generalisation there are others: ensembles can perform more complex
tasks than individual members, the overall system can be easier to
understand and modify and ensembles are more robust / degrade more
gracefully than individual predictors [249].
Working with an ensemble raises a number of issues. How to create or
select ensemble members? How many members are needed? When to remove
ensemble members? How to combine their predictions? How to encourage
diversity in members? There are many approaches to these issues, among
the best known of which are bagging [33,34]
and boosting [97,98,202].
Creating a good ensemble is an inherently multiobjective problem
[281]. In addition to maximising accuracy we also want
to maximise diversity in errors; after all, having multiple identical
predictors provides no advantage On the other hand, an ensemble of
predictors which make different errors is very useful since we can
combine their predictions so that the ensemble output is at least as
good on the training set as the average predictor
[165]. Hence we want to create accurate predictors with
diverse errors
[80,117,165,216,215]
In addition we may want to minimise ensemble size in order to reduce
run time and to make the ensemble easier to understand. Finally,
evolving variable-length chromosomes without pressure towards
parsimony results in bloat [231], in which case we have a
reason to minimise the size of individual members.
Although most ensembles are
non-evolutionary, evolution has many applications within ensembles.
i) Classifier creation and adaptation: providing the ensemble
with a set of candidate members. ii) Voting:
[169,272,273,71] evolve weights
for the votes of ensemble members. iii) Classifier selection:
the winners of evolutionary competition are added to the
ensemble. iv) Feature selection: generating diverse classifiers
by training them on different features (see §3.1
and [167] §8.1.4). v) Data selection:
generating diverse classifiers by training on different data (see
§3.1). All these approaches have
non-evolutionary alternatives. We now go into more detail on two of
the above applications.
Single-objective
evolution is common in evolving ensembles. For example,
[191] combines accuracy and diversity into a single
objective. In comparison, multi-objective evolutionary ensembles are
rare [69] but they are starting to appear
e.g. [2,69,68]. In addition to
upgrading GBML to multi-objective GBML other measures can be taken to
evolve diversity, for example fitness sharing e.g. [192]
and the co-evolutionary fitness method we describe next.
Gagné et al. [100] compare boosting and co-evolution
of learners and problems - both gradually focus on cases which are
harder to learn - and argue that co-evolution is less likely to
overfit noise. Their co-evolution inspired fitness works as follows:
Let Q be a set of reference classifiers. The hardness of a
training input 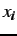 is based on how many members of Q
misclassify it. The fitness of a classifier is the sum of hardnesses
of the inputs
is based on how many members of Q
misclassify it. The fitness of a classifier is the sum of hardnesses
of the inputs 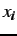 it classifies correctly. This method results in
accurate yet error-diverse classifiers since both are required to
obtain high fitness. Gagné et al. exploit the population of
classifiers to provide Q.
They also introduce a greedy margin-based scheme for selection of
ensemble members. They find that a simpler off-line version of their
EEL (Evolving Ensemble Learning) approach dominates their on-line
version as the latter lacks a way to remove bad classifiers. Good
results were obtained compared to Adaboost on 6 UCI
[9] datasets.
it classifies correctly. This method results in
accurate yet error-diverse classifiers since both are required to
obtain high fitness. Gagné et al. exploit the population of
classifiers to provide Q.
They also introduce a greedy margin-based scheme for selection of
ensemble members. They find that a simpler off-line version of their
EEL (Evolving Ensemble Learning) approach dominates their on-line
version as the latter lacks a way to remove bad classifiers. Good
results were obtained compared to Adaboost on 6 UCI
[9] datasets.
There are two extremes.
Usually each run produces one member of the ensemble and many runs are
needed. Sometimes, however, the entire population is eligible to join
the ensemble, in which case only one run is needed. The latter does
not resolve the ensemble selection problem: which candidates to
use? There are many combinations possible from just a small pool of
candidates, and, as with selecting a solution set from a Michigan
populations, the set of best individuals may not be the best set of
individuals (that is, the best ensemble). The selection problem is
formally equivalent to the feature selection problem [100]
§3.2. See e.g. [251,241] for evolutionary
approaches.
Research directions for evolutionary ensembles include multi-objective
evolution [69], hybrid ensembles [69]
and minimising ensemble complexity [192].
Key works include Opitz and Shavlik's classic 1996
paper on evolving NN ensembles [216], Kuncheva's 2004 book
on ensembles [167], Chandra and Yao's 2006 discussion
of multi-objective evolution of ensembles [68], Yao and
Islam's 2008 review of evolving NN ensembles [317] and
Brown's 2005 and 2010 surveys of ensembles
[37,35]. We cover evolving NN ensembles in §
3.4.



Next: Evolving Neural Networks
Up: GBML Areas
Previous: Genetic Programming
Contents
T Kovacs
2011-03-12