Assume that a rigid surface in a 3-D scene is moving relative to a
stationary camera and let points in the scene be defined with respect
to the camera reference frame, with the z-axis aligned with the
optical axis and the image plane lying in the xy-plane. As
illustrated in Fig 1, the origin is then
at the point where the optical axis cuts the image plane. For this
model, perspective projection of a 3-D point 
onto an image point 
is given by
where 
is the inverse focal length. In contrast to the
usual approach in which the origin is at the centre of projection,
this model decouples the representation of depth from that of the
camera, ie focal length, and this enables independent estimation of
both as in [1]. The 2-D motion
induced by the motion of a 3-D
point is then given by
Expressing the 3-D motion in terms of the
instantaneous rectilinear and angular velocities, 
and 
respectively, ie
then gives an alternate form of the basic motion equations:
where because of the difference in origin, depth and angular velocity are no longer decoupled, as they are for the usual camera model [4].
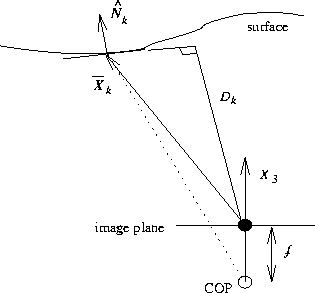
Figure 1: Camera and surface model
The structure model is based on the assumption that the scene consists
of smooth surfaces and that these can be modelled by piecewise planar
approximations, defined by sets of local normals and depths. Denoting
the unit normal of one such surface at a point 
by
, then combining the equation of the tangent plane, ie
with the projection model in eqn (1), the variation
in depth about the projected point 
can be approximated
by
where 
is the perpendicular distance
of the surface point from the origin as shown in
Fig. 1. Replacing 
with this expression in
equations (4) and (5) then gives a
non-linear expression for the motion field about in
terms of the spatial coordinates, 3-D motion, surface normal and focal
length. Denoting this expression by 
, where k
indicates the dependence on the local planar structure, a six parameter affine approximation to the motion field can be obtained by
linearising about the projection centre , ie
where 
is the Jacobian of
. Thus, for a rigid surface moving with motion
(or, alternatively, surfaces in a
static scene viewed by a moving camera), eqn (8)
defines an affine approximation to the motion field associated
with local patches on the surface. Note that the affine parameters are
non-linearly related to the 3-D structure and motion, hence the use of
an EKF for their estimation. This is considered in Section
4. How such affine estimates are obtained
from an image sequence is considered next.
