Introduction

The goal of this work is to determine the position and orientation of planar patches in a scene relative to the centre of the object to which they are attached. We have tackled this problem by developing a novel Kalman estimator for the 3-D position, normal orientation and motion of the patches, based on the 2-D affine estimates of motion within a 2.5-D representation. The estimator has the following key features:

1. For each planar patch, the affine motion parameters are equated with a local linearisation of the 2-D motion field about the projected patch centre. Given a set of such patches, this allows the estimation of arbitrary surface structure in terms of local normals and 3-D positions.

2. Recursive estimates of the structure (normals and 3-D positions) and 3-D motion over a sequence are obtained using an extended Kalman filter in which the local linearisations for a set of patches form the observation equation. This gives robust estimation for a relatively small number of patches (typically 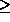8).

3. The 2-D motion field is defined using a camera geometry which decouples focal length from depth. This enables simultaneous estimation of the focal length within the filter and hence provides metric estimates of the structure without the need for pre-calibration, an obvious requirement when coding arbitrary sequences.

The estimator gives richer descriptions of surface structure than that provided by existing feature correspondence techniques, but obtained without the computational disadvantages of an optical flow scheme. As such, it provides a powerful and computationally efficient method of dynamically extracting structure from image sequences. A full description of the estimator and an analysis of its performance for both synthetic and real data is given in the remaining sections.