


Next: Arguments For and Against
Up: Introduction
Previous: Introduction
Contents
Subsections
1.1 Machine Learning
1.1 Machine Learning
Machine learning is concerned with machines which improve with
experience and reason inductively or abductively in order to:
optimise, approximate, summarise, generalise from specific examples to
general rules, classify, make predictions, find associations, propose
explanations, and propose ways of grouping things. For simplicity we
will restrict ourselves to classification and optimisation problems.
Inductive Generalisation
Inductive
generalisation refers to the inference of unknown values from known
values. Induction differs from deduction in that the unknown values
are in fact unknowable, which gives rise to fundamental
limitations in what can be learned. (If at a later time new data makes
all such values known the problem ceases to be inductive.) Given the
unknown values are unknowable, we assume they are correlated
with the known values and we seek to learn the correlations. We
formulate our objective as maximising a function of the unknown
values. In evolutionary computation this objective is called the
fitness function, whereas in other areas the analogous feedback signal
may be known as the error function, or by other names.
There is no need for induction if: i) all values are known and
ii) there is enough time to process them. We consider two inductive
problems: function optimisation and learning. We will not deal with
abduction.
1-Max: a Typical Optimisation Problem
The 1-max problem is to maximise the number of 1s in a binary string
of length 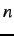 . The optimal solution is trivial for humans although it
is less so for EAs. The representation of this problem
follows. Input: none. Output: bit strings of length
. The optimal solution is trivial for humans although it
is less so for EAs. The representation of this problem
follows. Input: none. Output: bit strings of length 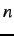 . Data
generation: we can generate as many output strings as time allows,
up to the point where we have enumerated the search space (in which
case the problem ceases to be inductive). Training: the fitness
of a string is the number of 1s it contains.
We can evaluate a learning method on this task by determining how
close it gets to the known optimal solution. In more realistic
problems the optimum is not known and we may not even know the maximum
possible fitness. Nonetheless, for both toy and realistic problems we
can evaluate how much training was needed to reach a certain fitness
and how a learning method compares to others.
. Data
generation: we can generate as many output strings as time allows,
up to the point where we have enumerated the search space (in which
case the problem ceases to be inductive). Training: the fitness
of a string is the number of 1s it contains.
We can evaluate a learning method on this task by determining how
close it gets to the known optimal solution. In more realistic
problems the optimum is not known and we may not even know the maximum
possible fitness. Nonetheless, for both toy and realistic problems we
can evaluate how much training was needed to reach a certain fitness
and how a learning method compares to others.
Classification of Mushrooms: a Typical Learning Problem
Suppose we want to classify mushroom species as poisonous or edible
given some training data consisting of features of each species
(colour, size and so on) including edibility. Our task is to learn a
hypothesis which will classify new species whose edibility is
unknown. Representation: the input is a set of nominal
attributes and the output is a binary label indicating edibility.
Data generation: a fixed dataset of input/output examples
derived from a book. Typically the dataset is far, far smaller than
the set of possible inputs, and we partition it into train and test
sets. Training: induce a hypothesis which maximises
classification accuracy on the train set. Evaluation: evaluate
the accuracy of the induced hypothesis on the test set, which we take
as an indication of how well a newly encountered species might be
classified.
Although many others
exist, we focus on the primary machine learning paradigm: standard
Supervised Learning (SL), of which the preceding mushroom
classification task is a good example. In SL we have a dataset of
labelled input/output pairs. Inputs are typically called instances, examples or
exemplars and are factored into attributes (also called features)
while outputs are called classes (for classification tasks) or the
output is called the dependent variable (for regression tasks).
In SL
we typically have limited training data and it is crucial to find a
good inductive bias for later use on new data. Consequently, we must evaluate the generalisation of the induced hypothesis from the
train set to the previously unused test set.
In contrast, in optimisation we can typically can generate as much
data as time allows and we can typically evaluate any output. We are
concerned with finding the optimum output in minimum time, and,
specifically, inducing which output to evaluate next. As a result no
test set is needed.
A great many issues arise in
SL including overfitting, underfitting, producing human readable
results, dealing with class imbalances in the training data,
asymmetric cost functions, noisy and non-stationary data, online
learning, stream mining, learning from particularly small datasets,
learning when there are very many attributes, learning from positive
instances only, incorporating bias and prior knowledge, handling
structured data, and using additional unlabelled data for training.
None of these will be dealt with here.



Next: Arguments For and Against
Up: Introduction
Previous: Introduction
Contents
T Kovacs
2011-03-12