GENERALIZATION
VS. DISCRIMINATION IN LEARNING
Tim Kovacs
Department
of Computer Science, University of Bristol
Bristol, UK
Andy J.
Wills
Psychology,
University of Exeter
Exeter, UK
Synonyms
[None]
Definition
Generalization and discrimination of observations is fundamental to all
learning. We provide an introduction to key issues in the context of Machine Learning (ML), with references
to the psychology literature, but can
only touch on the basics. A related article deals with this subject in
the context of comparative psychology and biology.
In ML, learning
is often conceived as the search for a hypothesis which is a good fit to
existing observations, on the assumption that it will also fit future
observations well (with “hypothesis” being a very inclusive term in ML, that
does not pre-judge the nature of the representation employed). However, there
are typically very many hypotheses which fit existing
observations well. A learner must therefore select which hypothesis to adopt,
and some are more general than others. We'll use the somewhat contrived example
of teaching a naēve learner to discriminate bluebirds from other birds. The
learner has no prior experience of birds (it might be a robot or an
extraterrestrial) and we teach it by pointing out birds and labeling them as
bluebirds or not bluebirds. Suppose we first point out a fairly dark bird at
mid-day and indicate that it is a bluebird. The learner might adopt the rather
general hypothesis that all birds are bluebirds, which we will call h1. This is
of course an overgeneralization, as the learner has not placed
enough restrictions on what qualifies as a bluebird. Overgeneralization is not
uncommon in human development (e.g. applying the label “doggie” to all
four-legged creatures; applying linguistic regularities to exception items,
e.g. “I go-ed to the park”). Conversely, the learner
might adopt the overly specific hypothesis that only fairly dark birds seen around
mid-day are bluebirds (h2), which places too many restrictions on what
qualifies as a bluebird. An overly specific hypothesis fits observations too
closely and we say that it overfits the
data. There is some evidence that one characteristic of disorders such as
autism is under-generalization of this sort.[1]
Finally, the learner might adopt any of a number of hypotheses of generality
between these two extremes, for example, that all dark birds are bluebirds
(h3). All three hypotheses are consistent with the single observed bird,
and nothing more can be learned from this observation. If the learner selects a
hypothesis, but new observations reveal it to be overly general
or overly specific, it should revise its hypothesis. For example, upon being
shown a white swan, the learner should no longer cling to h1, the overgeneral hypothesis that all birds are bluebirds. (Note
that it cannot disprove h1 if it only ever sees bluebirds – so called
“negative examples” are very useful!). Selecting a hypothesis is an inductive (as opposed to
deductive) problem, and any factor, other than observations, which contributes to
this selection is part of the learner’s inductive
bias. For example, it might be wary of overfitting its observations and
avoid very specific hypotheses, even if they are consistent. The receptors
through which information about observed objects is obtained may form part of
the inductive bias – both by making some information unavailable (e.g.
tones over about 20kHz for humans) and by substantial effects on perceived
similarity (e.g. difference between the trichromatic color vision of most
humans, the dichromatic vision of most other mammals, and the tetrachromatic vision of some birds).
The term
“generalization” is used in several related ways in reference to learning.
First, making inferences about later observations based on past ones is
referred to as generalizing. If the learner above is shown a new bird and asked
whether it is a bluebird, it must generalize from its past observations to
answer the question. Hence, except in the special case where the current
observation is identical to a previous one, all classification involves
generalization. We have already seen a second use of “generalization”: a
hypothesis which assigns observations to the same category is said to
generalize over them, whereas a hypothesis which assigns observations to
different categories is said to discriminate between them. There is also a
third use of the term. When a learner replaces its current hypothesis with a
more general one, it is said to generalize the hypothesis. The process of learning, to the extent that it is a matter of improving
accuracy or some other measure, is a matter of generalizing and specializing
hypotheses. Consequently,
a central concern for cognitive psychologists is to determine how a learner
generalizes, and a central concern for ML researchers is how to engineer learners which generalize appropriately.
Theoretical Background
In the bluebird
example, hypotheses involve two dimensions: time of day and shade. It can be helpful
to visualize low-dimensional hypotheses as decision boundaries as figure
1 does for the bluebird hypotheses.
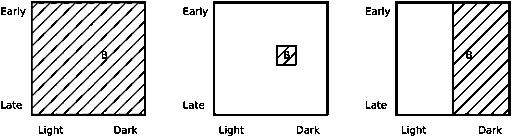
Figure 1. On the left is h1: all birds are bluebirds.
In the middle h2: only fairly dark birds seen around
mid-day are bluebirds. On the right h3: all dark
birds are bluebirds. In each case the first observed
bird (a fairly dark bird seen at mid-day) is shown
with a B (for Bluebird).
Note that,
while h2 as drawn is quite specific, we could have made it as small as a single
point, but that seemed less useful as both an illustration and as a basis for
learning. Note also that h3 completely ignores the time of day. On one hand it
might be irrelevant, since a given bird's species does not depend on the time
of day, but on the other hand, we might be more likely to encounter certain
species at certain times. In general, it is not trivial to determine which dimensions
are the most useful for learning; in ML this is called feature selection. Humans and other animals seem to track the
correlation between stimulus dimensions and outcomes (e.g. category labels)
and, over time, adjust the amount of attention these dimensions receive.
Now suppose
more birds are added as in figure 2 (left), with B for Bluebird and O for Other
bird. If we restrict our hypotheses to be rectangular, the smaller rectangle is
the most specific hypothesis consistent with the observations, while the larger
rectangle is the most general consistent hypothesis. Any rectangle within them will
also be consistent, and the selection of a particular consistent hypothesis by
the learner will be due to its inductive bias. Note that we have very few observations,
which can greatly increase the risk of overfitting and overgeneralizing. With
more observations we might find that the larger and smaller hypotheses were
much closer, and hence that there was less difference between the consistent
hypotheses. Note also that, in reality, bluebirds and other birds would tend to
overlap in our chosen 2-dimensional space. This would complicate matters
significantly, so, for simplicity, let us overlook it for the moment.
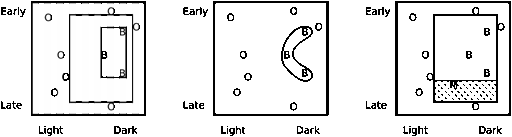
Figure 2. Left: the smallest and largest consistent
rectangles. Middle: a hypothesis which fits the
observed bluebirds more closely than any
rectangle. Right: a new, misidentified bird (M) reduces the
largest consistent rectangle.
The
restriction to rectangular hypotheses is a form of bias, as it heavily
constrains the generalizations which can be made. Why
might we use rectangles in ML? One reason is they are easy to define, both
geometrically and logically. Geometrically, we need only specify one corner and
two offsets from it. Logically, we need only give an interval for each dimension,
e.g. “all birds with shades between S1 and S2 and seen between 2pm and 4pm are bluebirds”.
We could, however, use a language which defines
circles, or indeed arbitrary shapes.
Given that
rectangles constrain the generalizations which can be
made, why not use arbitrary shapes? The example in the middle of figure 2
illustrates that a complex shape can fit the observed bluebirds much more
closely than any rectangle. However, as we noted earlier, we do not want to
overfit our observations, as that typically results in poor predictive accuracy
on future observations (that is, poor generalization). More complex hypotheses
are better able to fit observations than simpler, less flexible, hypotheses,
and are hence more likely to overfit them. Consequently, simpler, less flexible
hypotheses are often preferable, which gives us a basis for Ockham's razor, a well-known bias
which holds that we should prefer the simplest
hypotheses which fit the observations to date. The Minimum Description
Length principle is a formalization of Ockham's razor and an important
concept in information theory and computational learning theory.
Important Scientific
Research and Open Questions
Our bluebird example is simplified in a number of ways. Rectangular
hypotheses are often too inflexible and both ML systems and psychological models
use others. Humans and other animals do find it easier to learn hypotheses
whose bounds are parallel to psychologically meaningful dimensions, which is an
example of their inductive bias.
A very significant simplification, and bias, is that we ignored the
possibility of noise, which makes overfitting much more of a problem. By noise we
mean, for example, recording an incorrect time of day or shade, or mistaking a bluebird
for a non-bluebird. This last is shown in figure 2 (right) where the M
represents a new bluebird mistaken for a non-bluebird. This seriously reduces
the most general consistent rectangle, as shown with dashed lines. Because
noise is so common, practical learning methods cannot insist on fully
consistent hypotheses.
Another
simplification and bias was the
assumption that bluebirds can be defined by a single rectangle; in general,
concepts may require a set of such hypotheses. For example, “fairly dark birds
seen quite early or quite late”
requires two rectangles. Real-world categories are often considered to have a
family “resemblance” structure, in that they contain many properties that are
characteristic, rather than a set of properties that are singly necessary and
jointly sufficient.
Our bluebird example also lacks any mechanism for capturing the graded
nature of real-world categories. Chickens and penguins are both birds, but
people rate chickens as more typical of the bird category than penguins, and
can verify the accuracy of sentences such as “ a chicken is a bird” more
rapidly than sentences such as “a penguin is a bird”. People’s classification
of atypical items is also noisy, varying from day to day. For example, the
statement “a tomato is a vegetable” may be considered correct on one occasion,
but incorrect on the next. Hence, people’s categories can have fuzzy
boundaries. Other simplifications (and biases) in the example are that concepts
do not overlap and do not change over time.
We will not discuss methods (“algorithms”) by which machines learn, or
psychological models of learning, but there are many. Humans appear to have
access to multiple classification processes (e.g. rule extraction;
generalization from specific known instances). Further, the relative dominance
of those processes in determining people’s responses seems to be affected both
by the nature of the objects to be classified, and the amount of experience people
have of objects of that type.
In ML terms, our example is a case of supervised learning,
since the observed birds have been labeled by a teacher. Of course, very often
there is no teacher, in which case we have an unsupervised learning
problem, where the learner must optimize some criterion of its own choice. For
example, in clustering, the learner groups
observations into clusters based on their similarity, but the definition of
“similar” is left to the learner. Reinforcement learning is a
third paradigm, in which the learner responds to rewards and punishments. There
is also growing interest in newer paradigms, such as semi-supervised learning, which exploits both labeled and
unlabeled data. ML is finding many new applications, of which many involve
modeling human behavior, such as predicting customer preferences on websites,
or blocking unwanted email. Generalization and discrimination are slightly
different in each paradigm but nonetheless central to all.
Cross-References
Abstract concept learning in animals
Animal perceptual learning
Artificial learning and Machine Learning
Categorical learning
Classification learning
Concept formation
Concept learning
Concept learning of machines
Learning algorithms
References
Flach, P.
(forthcoming). Machine Learning. The
Art and Science of Algorithms that Make Sense of Data. Cambridge University Press.
Mitchell,
T. (1997). Machine Learning.
McGraw Hill.
Pearce, J.M. (2008). Animal learning and cognition: An
introduction. Psychology Press.
Pothos, E.M. and Wills,
A.J. (Eds.) (2011). Formal approaches in categroization. Cambridge University
Press.
Pearce
Russell,
S. & Norvig, P. (2003). Artificial
Intelligence. A Modern Approach.
Second editon. Prentice Hall.
Wills, A.J. (2011). Models of categorization. In D. Reisberg (Ed.). Oxford
handbook of cognitive psychology. Oxford University Press.
Appendix – Key Terms
Inductive
reasoning [an article]
Minimum
Description Length principle: an inductive bias used in machine learning which suggests that shorter (i.e. simpler)
hypotheses should be preferred.
Ockham's
razor: the heuristic that we should prefer the simplest hypotheses
which fit the observations to date.
Overfitting:
when a learner fits its training data too closely, and does not draw conclusions which are as general as they should be.
Overgeneralization:
when a learner draws inappropriately general conclusions from its training
data.
Reinforcement
Learning [an article]
Semi-supervised
Learning. Obtaining labeled data for supervised learning can be costly, but often large amounts of unlabeled data can be obtained
cheaply. Semi-supervised learning exploits both at once and is useful when only
limited labeled data is available.
Supervised
Learning [an article]
Unsupervised
Learning [an article]